Exercices en Electricité I

Module de Physique : Electricité I

Soit deux vecteurs u et v

tels que:

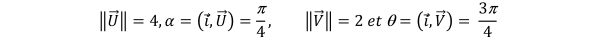
• Représentez les vecteurs dans le plan

• Calculez les coordonnées cartésiennes de U et V dans la base

• Calculer le produit scalaire de U.V

.

Calculer en prenant le repère le plus approprié:

1. La surface d’un rectangle de largeur a et de longueur b
2. Le périmètre et la surface d’un disque de centre O et de rayon R
3. Déterminer les éléments de la surface latérale dS et du volume dV d’un cylindre C d’axe Oz de rayon R et de hauteur h
4. En déduire sa surface S et son volume V
5. Déterminer les éléments de surface dS et de volume dV d’une sphère de centre O et de rayon R
6. En déduire sa surface et son volume

On considère un cône d’axe OZ, de sommet O et de demi angle au sommet α .

1. Calculer la surface S de la calotte sphérique définie par l’intersection du cône avec une sphère de centre O et de rayon R.
2. Déduire l’angle solide sous lequel on voit la surface S à partir du point O, en fonction de α.
3. Déduire l’angle solide sous lequel on voit tout l’espace.

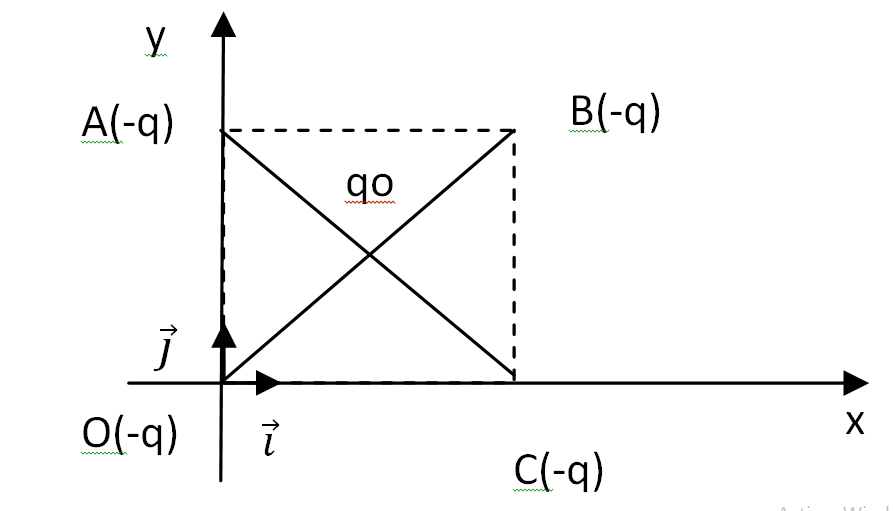
Quatre charges ponctuelles identiques –q (q > 0) sont fixées aux sommets A, B, C et O d’un carré de côté a. Une cinquième charge q0 > 0 est maintenue fixe au centre D du carré.

1. Déterminer  la force exercée sur la charge qo ?
2. Déterminer l’expression de force exercée sur la charge -q placée en O ?
3. Déterminer la valeur de q0 en fonction de q pour que cette force électrostatique soit nulle.

Soit  un cylindre d’axe Oz de rayon R et de hauteur h chargé uniformément en surface avec une densité surfacique de charges σ .

1. Déterminer le champ élémentaire dE(M) crée par un élément de surface dS du cylindre chargé en un point M d’abscisse z de l’axe Oz
2. En déduire le champ total

Considérons deux sphères S1 et S2 de même centre  O et de rayons respectifs R1 et R2 (R1<R2). La sphère interne S1 est chargée uniformément en volume avec une densité volumique de charges r et la sphère externe S2 est chargée uniformément en surface avec une densité surfacique de charges σ .

1. En utilisant la symétrie de charges déterminer la direction du champ E(M) crée par les deux sphères en un point M de l’espace ?
2. En utilisant la notion des invariance montrer que le champ E(M) ne dépend que de la distance r = ||OM|| ?
3. Quelle est la surface de Gauss adaptée à cette distribution de charges ?
4. En appliquant le théorème de Gauss, déterminer le champ E(M) crée par les deux sphères en tout point M(r ) de l’espace càd pour : r<R1, R1<r<R2 et r>R2
5. Déterminer le potentiel V(M) pour les trois cas ? (V(∞)=0)

Considérons deux cylindres C1 et C2 de même axe Oz de rayons respectifs R1 et R2 (R1<R2) et de hauteur infini. Les deux cylindres sont chargés uniformément en surface avec les densité surfacique de charges respectifs σ 1 et σ 2.

1. En utilisant la notion de symétrie de charges déterminer la direction du champ E(M) crée par les deux sphères en un point M de l’espace ?
2. En utilisant la notion des invariance montrer que le champ E(M) ne dépend que de la distance r = ||OM|| ?
3. Quelle est la surface de Gauss adaptée à cette distribution de charges ?
4. En appliquant le théorème de Gauss, déterminer le champ E(M) crée par les deux sphères en tout point M(r ) de l’espace càd pour : r<R1, R1<r<R2 et r>R2
5. Déterminer le potentiel V(M) pour les trois cas ? (V(0)=0)