TD de Thermodynamique II
Exercice 1 : Ecoulement d’un fluide
Dans un volume de contrôle , un fluide pénètre en 1 à la vitesse v1 et à l’altitude z1 et ressort en 2 à la vitesse v2 et à l’altitude z2 (figure ci-contre). Entre les instants t et t + dt, une masse dm1 de fluide entre dans le volume de contrôle et une masse dm2 en ressort. | 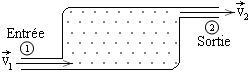 |
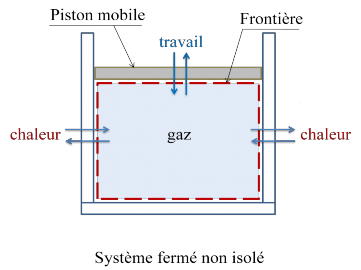
Le système, délimité par la frontière , reçoit de l’extérieur une énergie chaleur et une énergie travail autre que le travail des forces de pression.
1) Déterminer la variation d’énergie interne totale entre les instants t et t + dt.
2) En déduire qu’en régime permanent, et si le système ne reçoit de l’extérieur ni chaleur ni travail, on a :
3) Déduire la vitesse v d’écoulement d’un gaz parfait à la sortie d’un mince tube horizontal, si la vitesse du gaz à l’entrée de est négligeable, et ses températures sont T1 = 300 K à l’entrée et T2 = 295 K à la sortie.
Données : Masse molaire du gaz : M = 28 g.mol-1 ; Rapport des chaleurs spécifiques : = cp/cv = 7/5 ;
Constante universelle des gaz parfaits : R = 8,314 J.mol-1.K-1.
Exercice 2 : Chaleur latente de vaporisation
Un cylindre muni d’un piston susceptible de se déplacer sans frottement contient une mole de vapeur d’eau à l’état surchauffée. Les parois du cylindre sont conductrices d’énergie chaleur et sont placées dans un bain thermostaté dont on peut régler la température. La vapeur d’eau pourra être assimilée à un gaz parfait jusqu’à l’état de saturation.
1) La température étant maintenue constante à T0 = 300 K, on comprime la vapeur de manière réversible et isotherme du volume V0 = 3 m3 au volume V1 = 0,63 m3. La vapeur se trouve alors partiellement liquéfiée et la pression est P1 = 1300 Pa.
a- Calculer le volume V » où apparaît la première gouttelette de liquide.
b- Déterminer l’énergie travail mise en jeu lors de la compression de la vapeur
c- Le volume massique de l’eau liquide est v = 1 cm3.g -1, calculer en mole, la quantité de vapeur d’eau dans l’état P1, V1.
2) Le volume étant fixé à V1, on élève la température de T0 à T. La chaleur latente de vaporisation de l’eau est supposée fonction linéaire de la température : ℓ = aT + b (a = – 48,66 J.mol-1.K-1, b = 56587 J.mol-1)
a- En négligeant le volume molaire de l’eau liquide devant celui de la vapeur, montrer que la pression de vapeur saturante est liée à la température par la relation : .
b- Trouver une relation donnant la température T2 à laquelle la phase liquide disparaît (on calculera une valeur approchée de T2 en posant T2 = T0 + δT et en considérant δT << T0).
Exercice 3.3 : Remplissage de bouteilles de gaz
Un réservoir métallique indéformable de volume V0 = 20 ℓ contient une masse m0 = 12 kg de Fréon 12 (CF2Cl2) à la température T0 = 10 °C.
1) Déterminer l’état thermodynamique (P0, v0, T0, h0) du Fréon 12 en ce point M0.
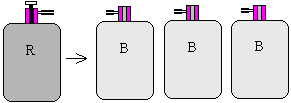
Comme indiqué sur la figure, le réservoir R sert pour remplir en vapeur de Fréon 12 saturée, une par une, des bouteilles de même volume V0 et contenant initialement du Fréon 12 à la température T0 et sous une pression Pb = 1 bar chacune. Ces remplissages se font à la même température T0 pour une ouverture du robinet r jusqu’à équilibre de pression.
2) Déterminer l’état thermodynamique (P1, v1, h1) du fluide dans le réservoir après le remplissage d’une bouteille. Calculer la masse de Fréon 12 restant dans R.
3) Calculer le nombre maximum n de bouteilles à remplir en vapeur de Fréon 12 saturée.
4) Déterminer l’état thermodynamique (P2, v2, h2) du fluide dans le réservoir R après le remplissage des n bouteilles. Calculer la masse de Fréon 12 restant dans le réservoir.
5) Le réservoir R est ensuite mis en communication, encore une fois, avec une autre bouteille identique aux précédentes, déterminer l’état thermodynamique (P3, v3) du fluide dans le réservoir R.
6) Déterminer qualitativement, sur le diagramme P-v, la position des points M0, M2 et M3 représentatifs des états du fluide.
La vapeur de Fréon 12 peut être assimilée à un gaz parfait.
On donne : masse molaire du Fréon 12 : M = 121 g.mol-1 ;
constante molaire universelle des gaz parfaits : R = 8,314 J.mol-1.K-1.
Etat de saturation du Fréon 12 à T = 10 °C :
T (°C) | P (bar) | v ‘ (m3.kg-1) | v » (m3.kg-1) | h’ (kJ.kg-1) | h » (kJ.kg-1) |
10 | 4,23 | 7,34.10-4 | 4,2.10-2 | 428 | 578 |