EPREUVE D’OPTIQUE

EPREUVE D’OPTIQUE (SMP2, SMC2)

Durée : 1h30

I- Questions de cours :

1-  Donner les conditions de Gauss.

2- Indiquer si les affirmations suivantes sont exactes ou non (répondre par oui ou non) :

a. Un dioptre plan est rigoureusement stigmatique.

b. Dans un prisme, le bleu est moins dévié que le rouge.

c. La vitesse de la lumière est plus faible dans l’eau que dans l’air.

d. Un miroir plan donne d’un objet réel une image virtuelle.

e. Pour une lentille mince divergente, un rayon issu de l’infini ressort de la lentille en passant par le foyer objet.

3- Montrer les propositions suivantes :

a- Le miroir concave ne donne jamais d’image virtuelle d’un objet virtuel.

b- Le miroir convexe ne donne jamais d’image réelle d’un objet réel.

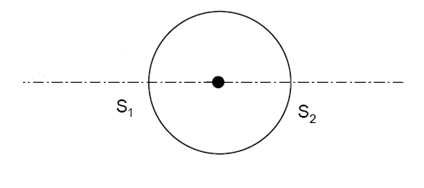
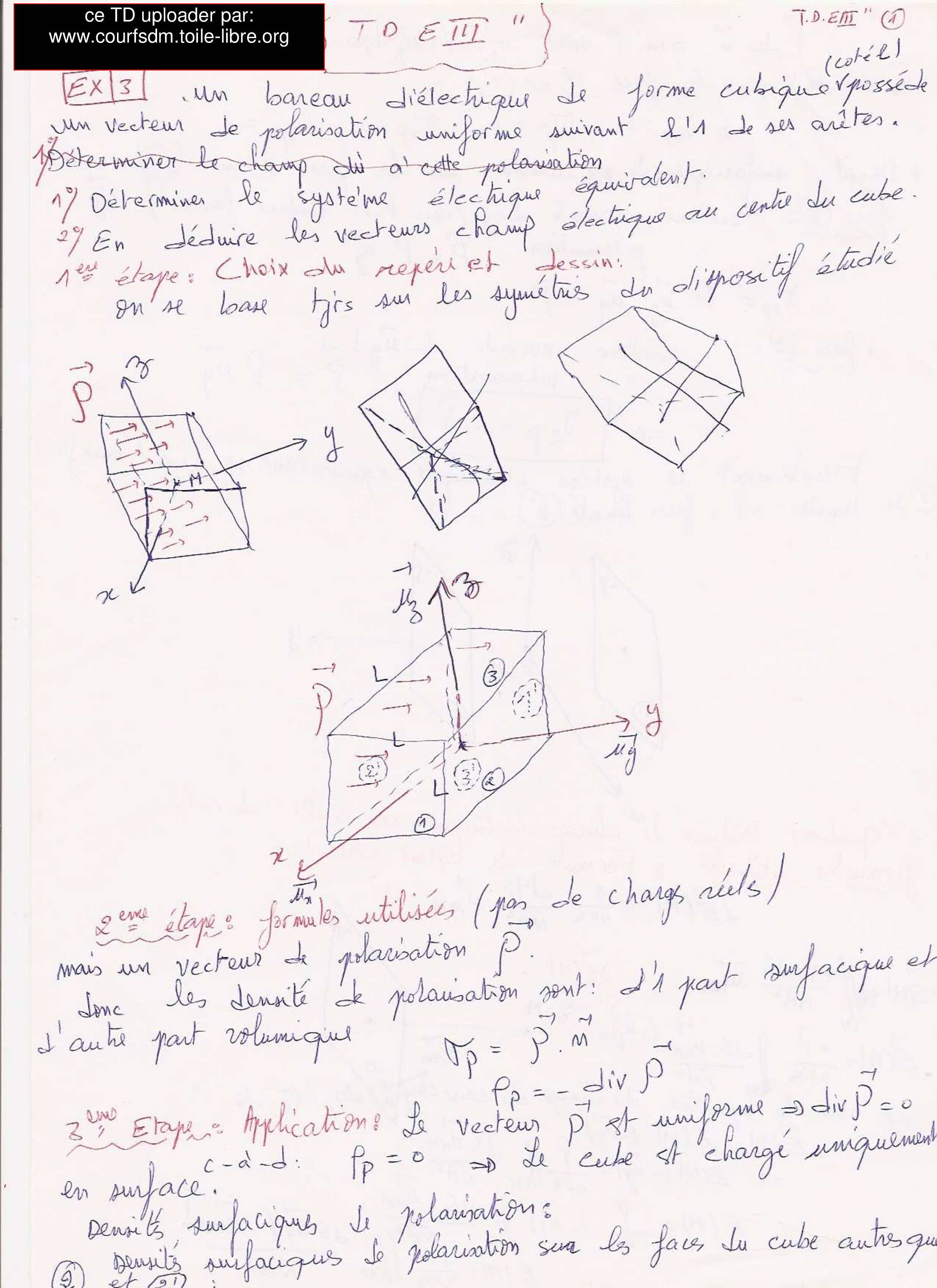
II – On considère un système centré constitué par une lentille boule de centre C (Figure 1), de rayon R = 5 cm et d’indice n = 1.5, plongée dans l’air. Soit AB un objet et A′B′ son image à travers le système dans les conditions de l’approximation de Gauss.

1. Ecrire, en prenant l’origine au centre, les formules de conjugaison de position et de grandissement de chacun des deux dioptres.
2. En déduire les positions des foyers (F₁, F′₁) et (F₂, F′₂) des deux dioptres. Faire l’application numérique.
3. Etablir la formule de conjugaison de position et de grandissement du système centré. Quel est alors le système optique équivalent à la lentille boule ? Préciser sa distance focale image f′.
4.  En déduire sa distance focale objet f, sa vergence V et sa nature.
5. Trouver la position par rapport à C, des foyers objet F et image F′ du système (S).   
6. Calculer la position du centre optique O de (S).
7. Tracer la marche d’un rayon passant par C. Conclure.
8. Calculer la position des points principaux H et H′ du système.
9. Déterminer la position des points nodaux N et N′ du système.
10. Retrouver  les positions de (F, H) et (F′, H′) par construction géométrique.
11. Un objet placé à 15 cm avant F (FA = – 15 cm). Calculer la position de l’image et le grandissement donnée par cette lentille :
12. En utilisant les formules de conjugaison et de grandissement avec origine aux foyers.
13. Par construction géométrique, en utilisant les éléments cardinaux du système.    
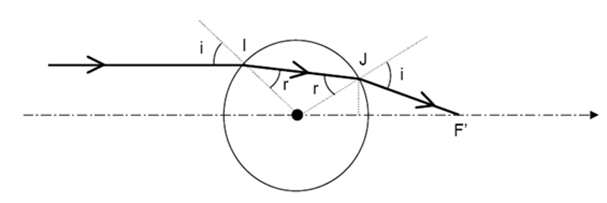
14. On veut maintenant retrouver l’expression de f′ (Figure 2) directement à partir des lois de Descartes, toujours dans l’approximation de Gauss. On suppose donc K et S₂ confondus et on identifie la tangente et le sinus d’un angle à cet angle.
15. Déterminer les angles du triangle CJF′ en fonction de n et r.
16. Déterminer la distance KF′ en fonction de R et n, puis la distance focale f ‘ toujours en fonction de R et n. Comparer avec le résultat obtenu à la question 3-